Unless your model domain is of global scale, you must choose some artificial boundary where your model-grid ends. Boundaries are areas of discontinuity that can negatively affect numerical solutions. Fortunately, there are methods available that serve to limit the detrimental effects boundary conditions can have on model results. Still, it is important to choose a model domain that is sufficiently large enough to keep these areas far from the features you intend to study.
Boundary conditions
Below is a brief discussion of some of the boundary conditions commonly employed in atmospheric models. These are periodic, rigid, dampened, and sponge boundaries.
Periodic
A periodic boundary condition is an effective solution for avoiding the boundary discontinuity problem completely. Using finite differencing techniques, here the Leapfrog scheme with an Asselin filter of 0.1, a solution is found for all values along x except the first (left-most) and last (right-most) grid points. The first grid point is set to the solution of the second-to-last grid point. The last grid point takes the value found for the second grid point.
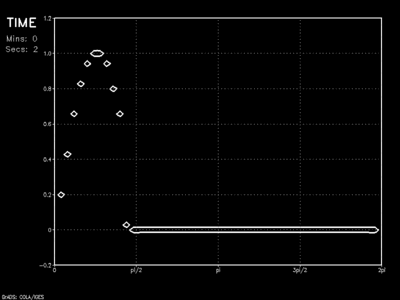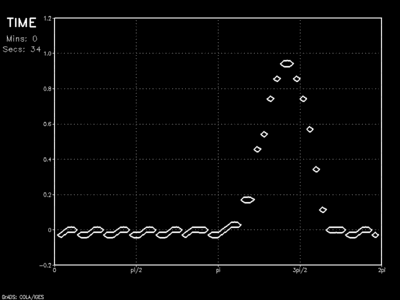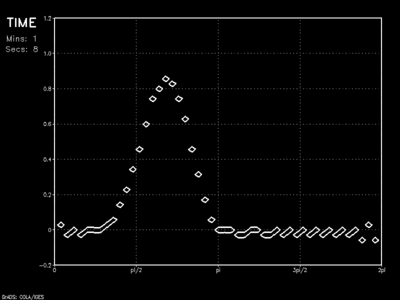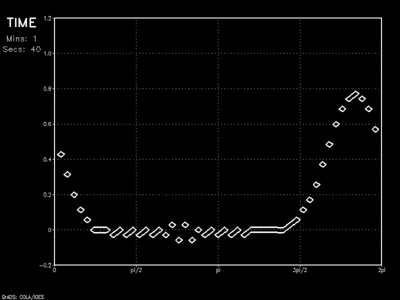
In this way there are no boundary conditions, thus no discontinuity. This would work seamlessly for global-scale east-west boundaries (though not for north-south boundaries) given a cylindrical map projection of the earth. This would not be appropriate, however, for any situation where it is unrealistic for a feature moving from left to right to again appear on the left.
Rigid
If we were to consider a high-resolution simulation of some local effect, a periodic boundary condition is precluded from use. What would happen then if we set the first and last grid point (boundary) values to zero? This would effectively end any of the unrealistic periodic looping effects passed between east and west boundaries.
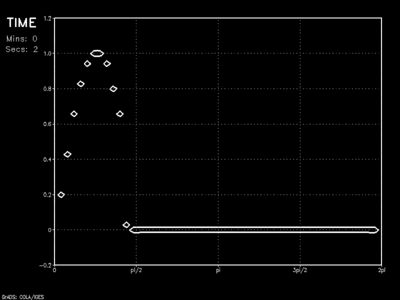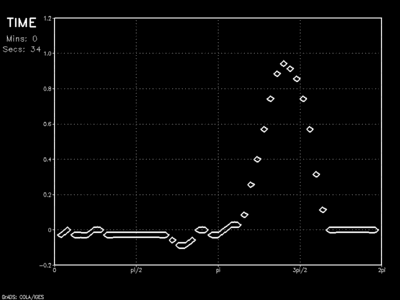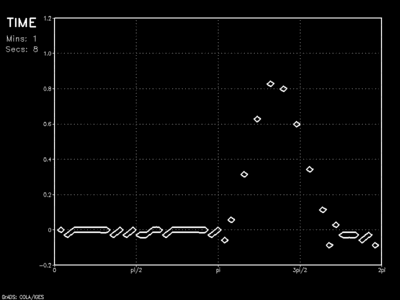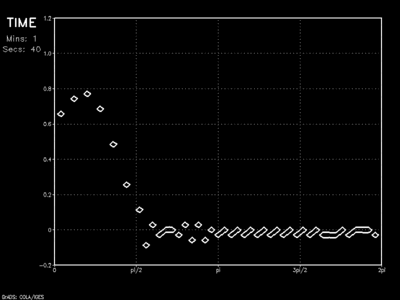
This rigid boundary solution has problems, however. In this case, the rigid wall acts as a mirror. The wave essentially reflects off of the boundary and travels back across the domain. This would result in mutual interference of waves and undesirable solutions.
Dampened
A dampened layer is akin to a rigid boundary with 1Δx padding. The reflection problem inherent with the rigid wall occurs because the solution does not address what drives the wave in the first place: the spatial derivatives between grid points. Here, endpoints on either side are set to solutions found at grid points adjacent to the boundaries. This effectively cuts the spatial differential in half.
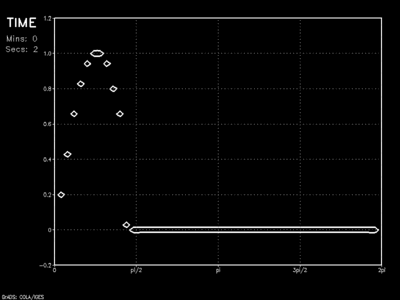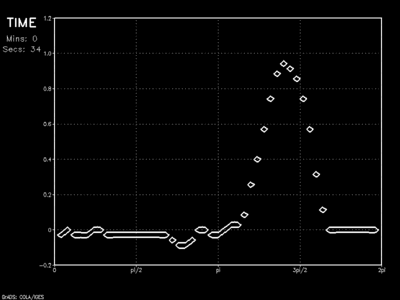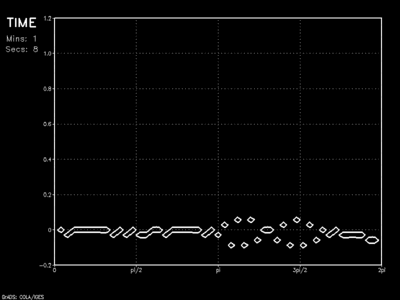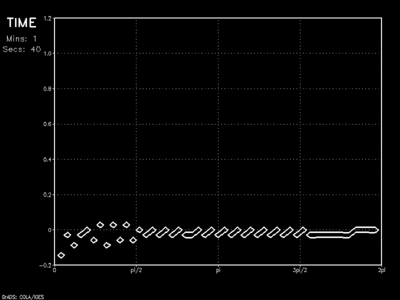
While a reflection problem is still clearly evident, the initial wave is reduced significantly upon rebound, and a much weaker anomaly travels back across the model domain. The sponge layer (below) takes this idea one step further.
Sponge layer
Noting the significant benefit gained by transitioning from rigid boundary to dampened, the sponged layer advances this concept to its natural conclusion. Rather than suppress the wave impulse across a thickness of only 1Δx, the sponge dampens over a much larger layer.
The animation shows the wave as it encounters a linear sponge of thickness 10Δx. Results show vast improvement on the dampened solution as barely a hint of the initial wave rebounds into the model domain.
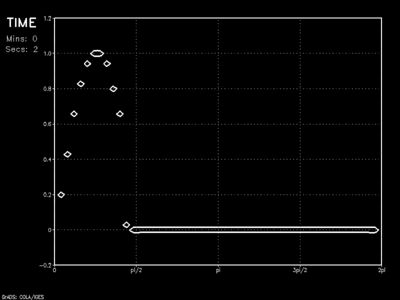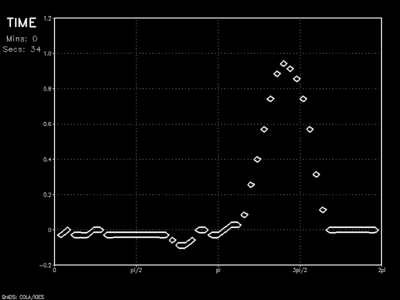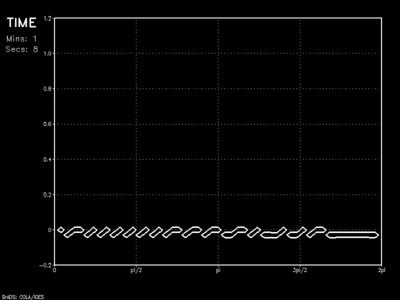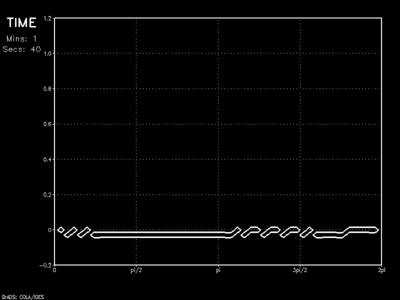
The sponge layer can, in fact, be further improved with the adoption of a more logarithmic onset. In this case, the sponge would act more gently at its outermost layers, with most of the absorption (ie: wave suppression) occurring in the middle.
The sponge boundary conditions effectively keep the study domain free from any interference caused by features that hit the edge of the model domain. This fact made it the obvious choice for my experiments.