Projects: Fortran

A programming language for numeric computation and scientific computing

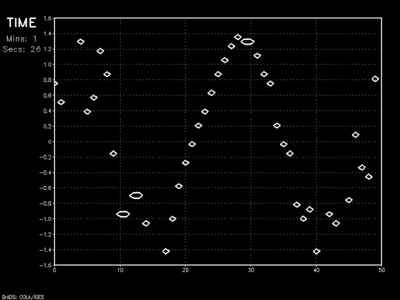
3D Artillery Game

I recalled an old turn-based two-player computer game where players took turns firing missiles at each other’s base. You would specify the angle of fire and the game would trace out the path of the projectile through the air as gravity pulled it down to the surface to explode. It was a two-dimensional game that would randomly seed base positions atop varying topography. I set for myself the goal of coding this game in three dimensions. As a classically trained meteorologist, I also added air resistance and random wind fields.

Public

Thesis

This was a study that examined the effect of the Appalachian Mountains on the precipitation distribution of tropical cyclones that impinge upon them. With the help of my advisor, Anantha Aiyyer, I began by classifying the 28 storms that passed through our study area between 1979 and 2006 into four general track types. I analyzed the track composites resulting, examined individual case studies, and ran numerical simulations with topography (control) and without (experimental) to isolate the effects of the Appalachians.

Numerical Model

In a class taught by Dr. Matthew Parker, I was required to code a numerical model and later use it for a mesoscale (ie: greater in extent than storm-scale) scientific experiment. I first hardwired flux form advection, leapfrog time differencing, and lateral sponge boundaries into the code. I later added Asselin filtering, artificial diffusion, Rayleigh dampening, and Kessler microphysics.

Boundary Conditions

Unless your model domain is of global scale, you must choose some artificial boundary where your model-grid ends. Boundaries are areas of discontinuity that can negatively affect numerical solutions. Fortunately, there are methods available that serve to limit the detrimental effects these discontinuities can have on model results.

Here is a brief discussion of some of the boundary conditions commonly employed in atmospheric models. These are periodic, rigid, dampened, and sponge boundaries.

Finite Differencing

Finite differencing is an explicit numerical means of solving spatial and temporal derivatives. I’ll show you the math that allows us to predict the future!

Come with me on a fantastic journey through time and space!